Projections in ArcGIS (Week 6)

The process of converting a spherical model onto a planar mode (while preserving certain spatial characteristics, such as distance, area, or shape) is known as map projection. Typically constructed by projecting from within the sphere, map projection enables the creation and utilization of accurate flat maps. With all of its benefits, it must be noted that there is not one map projection type can accurately translate all the spatial characteristics from the sphere to the plane. As a result, we have different projection types which are conformal, equidistant, and equal area, with each having their own distinct advantages and disadvantages that are used accordingly. All these different types of maps, regardless of their accuracies and inaccuracies, enable the convenient representation of maps on a planar surface, conducive to easy distribution and storage of maps that would not be possible with globes.


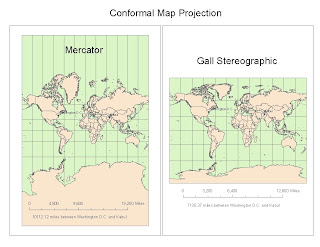
Certain conformal map projections, such as Mercator and Gall stereographic above, are able to preserve both shape and local angles, creating a system of orthogonal latitude and longitude gridlines. Mercator maps in particular represents rhumb lines derived from an initial bearing as straight lines, and stereographic preserves the shape of circles. On the other hand, conformal maps distort areas which are made obvious by the disproportionate size of Antarctica in both the Mercator and Gall stereographic examples. Equidistant map projections, such as cylindrical and conic shown below, represent accurate distances along designated lines and outward from the center. Unfortunately this type of projection significantly distorts area sizes, and does not necessarily show true distances of the points along the center as we can see in the inaccurate distance between the Americas and Australia in the equidistant conic example. Equal area map projections, such cylindrical and sinusoidal shown below, preserve respective areas but also fail to accurately represent latitude-longitude grid angles. Cylindrical, also known as a Gall-Peters projection, only represent true distances along the 45th parallels north and south. On the other hand, sinusoidal represents the area of the Earth as the area between two symmetrically rotated cosine curves. From both, we can clearly see cylindrical and sinusoidal equal area examples that these gridlines are distorted, simply by comparing both to the conformal Mercator example.

For the purpose of this week's lab, we measured the distance between Washington, D.C. and Kabul and we clearly see the distinctions and differences between the various types of map projections. To determine bearing we can look at both the Mercator and Gall Stereographic conformal map projections. We see that the linearity in all directions dictates that traveling southeast in a straight line will conveniently get me from D.C. to Kabul. To determine true distance, we can look at both cylindrical and conic equidistant map projections. We can also see that mapping of longitudes and latitudes illustrates that the true distance between D.C. and Kabul is around 5,065 to 6,941 miles. And as the name alludes, we can accurately assess the areas of the United States and Afghanistan by referring to both cylindrical and sinusoidal equal area projections. I am certain that interchanging any of these map projection types with the data we are seeking will only result in false measurements.

All map projections have both positive and negative outcomes which depend on what information is being sought. Since it is impossible to accurately translate all spatial data from into a sphere and then to a plane, each projection will preserve some characteristics while significantly distorting the rest. As mentioned before, each map projection has its specific and proper use, which is why any spatial analysis can be rendered erroneous if the wrong type of projection is chosen. This is the reason why it is imperative to be aware of how each map projection was created, what its intention is used for, and what spatial data it excels in translating from the three dimensional to the two dimensional domain.